このページは主に理系の大学生に非線型システムの初歩を学んでもらう目的で作成しました。
大学教育において気候システムや大気の運動の話をするとき、時々「非線型」ということばを使いますが、突然、非線型といわれても、あまり理解できないようです。このようなどの分野にも関わる学際的な概念というのは、実は学ぶ機会が少ないのかもしれません。
この世界は非線型な事象で満ちあふれています。しかし、人が物の理を理解しようとするとき、ありのままの非線型なかたちでは理解しにくい場合がほとんどです。特定の視点でのごく限られた近傍では、人が理解しやすいかたち(=線型)で近似できることがあります。そうすることによって、着目する事象の限定された範囲での性質を理解できます。そのような見方、考え方は線型化と呼ばれます。線型化することで、数学的に解析解が得られやすいという利点もあります。
しかし、本来、非線型な現象であるものを近似して線型化しているわけですから、その現象にとってより重要な本質や全体像は見えていないかもしれません。いくら線型化できる要素に分割したとしても、それらを統合した全体は、本来の非線型を本質とする全体とは全く異なる、つまらないものになっているかもしれません。このような考え方は科学思想におけるホーリズムにも通じます。それはさておき、本来は実際に起こる非線型現象を目の前で見ることができれば良いのですが、ここでは簡単なシミュレーションを通じて、非線型な現象のフレーバーを感じてもらえれば幸いです。
振り子と等時性
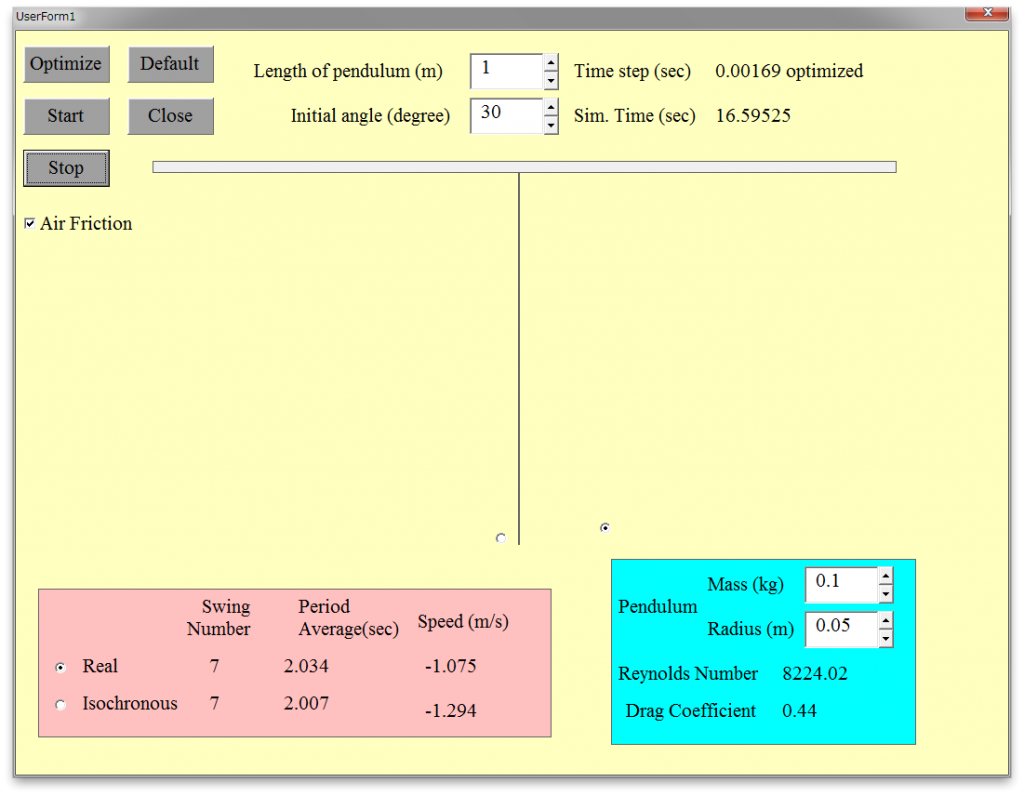
線型と非線型、部分と全体という意味を理解するために、最も簡単で身近な例になるのが、振り子です。振り子の等時性は小学校でも学びます。そして、高校や大学で学ぶ初等物理においても、「なぜ振り子の振動周期は振れ幅によらず『ほぼ』一定なのか?」という等時性に関する問いに対して、線型化した運動方程式によってその問いに答えられることを理解します。はじめから線型化ありきの論法で、解析解が得られ、振動周期は重力加速度とひもの長さだけに依存する、したがって、周期はおもりの重さや振れ幅に関係なく一定である、というスッキリした結論は、「本当は振り子の周期は振れ幅に依存している」という事実を忘れてしまいそうです。本来の振り子は、力が変位に比例しているわけではない非線型の関係になっており、普通に振らせれば「等時性がなりたたない」のが本来の姿です。もしも、小学校の理科実験で、いろいろな振れ幅で正確な実験をしてみたら、実は周期が一定ではなかった、という事実に気がつくでしょう。「本当は周期は何で決まっているのだろう?」と疑問を抱き、ゼロ点近傍に限定されない、振り子運動の全体像を理解しようとすれば、非線型の運動方程式と向き合う必要があります。
(振り子のシミュレーションの画面)
振り子のシミュレーション用エクセルファイル pend_sim.xlsm
ローレンツシステム
地球表層の大気も海も流体です。その動きの複雑さからも判るように、流体の運動の本質は非線型性だと言えるでしょう。非線型数理モデルとして、おそらく最も有名な「ローレンツ方程式」も、気象学者であるローレンツが、大気の運動を表現したものです。あまりにもシンプルすぎる方程式でありながら、特定の条件でカオス的な挙動を示し、しかし完全なランダムではない美しい構造(ストレンジアトラクタ)を持ちます。この単純な数理モデルの出発点は、一定の深さの流体について下端と上端に一定の温度差を与えた時に起こる対流運動です。ローレンツは、対流の運動と熱輸送の支配方程式から出発して、3つの変数X、Y、Zの単純な連立微分方程式に変形しました。一般的な非線型数理モデルやカオス理論の解説では、それらの変数の意味には触れていないことが多いのですが、それらにはしっかりと物理的な意味があります。ローレンツの論文によれば、Xは対流運動の強さ、Yは上昇流と下降流の間の温度差、Zは温度の鉛直分布の直線性からのひずみにそれぞれ対応しています。およそ50年前に発表された当時のこの研究では、LGP-30という真空管を使ったコンピュータによって、時間積分の1ステップの計算に1秒かかったと述べられています。しかし、後にストレンジアトラクタの一つと呼ばれるようになった位相空間トラジェクトリ(ローレンツ・アトラクタ)の計算結果がしっかりとその論文に示されています。
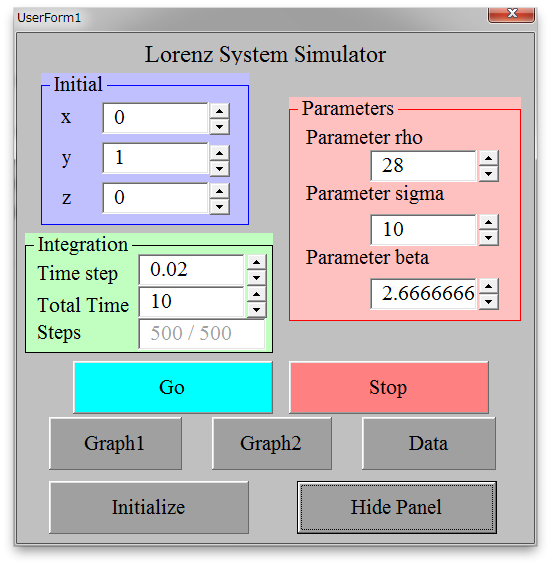
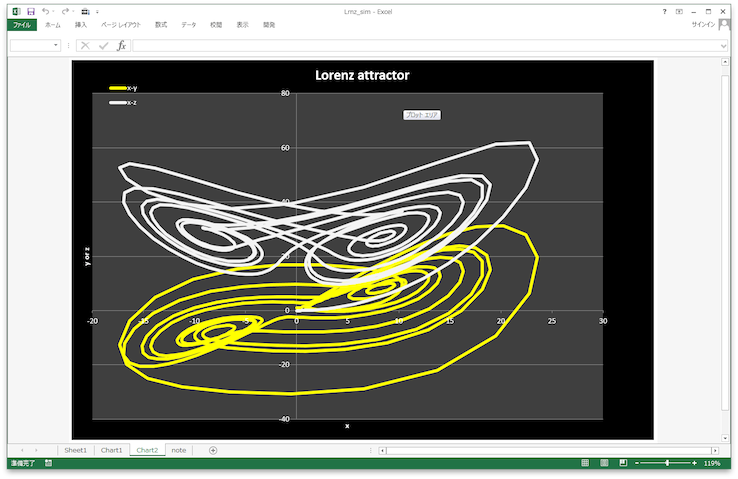
(設定画面と計算されたストレンジアトラクタ)
ローレンツシステム シミュレーション用エクセルファイル Lrnz_sim.xlsm
ローレンツシステム(3D描画機能あり) シミュレーション用エクセルファイル Lrnz_sim_3D.xlsm
ロトカ・ヴォルテラ方程式(捕食-被食関係)
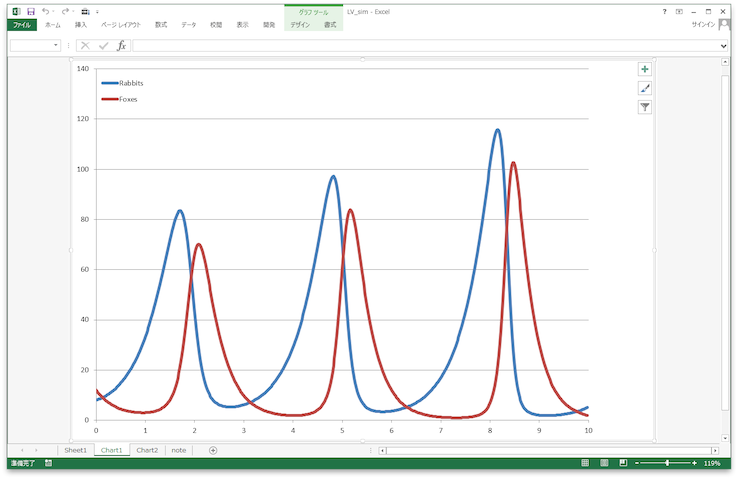
非線型な現象は物理だけの話ではなく、自然界の全ての分野に存在します。最近、ふと中学校の理科の教科書を見たら、カナダとアラスカの森林地帯におけるオオヤマネコとカンジキウサギの100年間の個体数変化のグラフが載っていました。相互に約10年周期で増減を繰り返す振動現象が示されています。まさに捕食者と被食者の相互作用が読み取れます。このような関係を独立な研究によってそれぞれ同様な数理モデルで再現できることを示したのが、Alfred J. LotkaとVito Volterraです。そのため、その関係式は両者の名をとり、Lotka-Volterra方程式と呼ばれており、生物学の中の数理生物学、特に個体群動態(population dynamics)の研究に大きな足跡を残しました。その式は、ローレンツ方程式と同じように、極めてシンプルな二変数の非線形連立微分方程式になっています。たったこれだけの数理モデルで、自然に個体数の振動現象が現れるのですから不思議です。
(設定画面と計算された個体数の変動)
ロトカ・ヴォルテラ方程式シミュレーション用エクセルファイル LV_sim.xlsm
ベローソフ・ジャボチンスキー反応(B-Z反応)
次は化学の非線型を取り上げましょう。複数の反応物が化学反応を起こすとき、その反応速度式には、例えば k[A][B]のように、それぞれの反応物の濃度どうしの積の項が含まれます。反応速度式は反応物の濃度の時間に関する微分方程式ですから、このような複数の反応物が関係した化学反応は本質的に非線型であり、それぞれの反応物の濃度の時間変化は、非線形連立微分方程式で表されることが容易に想像できます。余談ですが、例えば、大気化学のモデリングの研究では、何百という化学成分の何百という反応を、全地球の大気を細かく分けたグリッドごとに計算します。つまり、巨大で複雑な非線形連立微分方程式を解いていることになります。話を戻して、たとえ反応システムが非線型であるとしても、単に反応物が不活性な反応生成物に変化していくだけならば、反応物の濃度が時間とともに減ってゆくか、あるいは、いずれかの反応物がなくなってしまうことで、反応が止まってしまうだけかもしれません。しかし、もしも反応生成物がその反応の反応物を再生産するような働きをもっていたらどうでしょうか。このような反応は、自己触媒反応と呼ばれています。B-Z反応はこの自己触媒反応の一つとして知られています。一定の条件が整った場合、濃度が時間的に振動するような反応が起こり得ます。さらに、この反応をシャーレの中などで起こし空間的な濃度の変動に注目すると、美しい同心円状の模様(ターゲット・パターン)やスパイラル模様が現れることが知られています。物質の濃度が空間的に不均質であるとき、その濃度勾配を解消する向きに拡散が起こります。つまり、拡散と自己触媒反応の組合せによって自然に特定の構造が発現することを意味します。これは散逸構造と呼ばれるもので、非平衡状態における自己組織化とも言われます。数学的には、反応拡散方程式として、非線形連立偏微分方程式になります。エクセルでのシミュレーションでも判るように、はじめは完全にランダムで無秩序な状態から出発しているのに、時間とともに自然に構造が生み出されます。まさに、イリヤ・プリゴジンの「混沌からの秩序」そのものを見せてくれます。
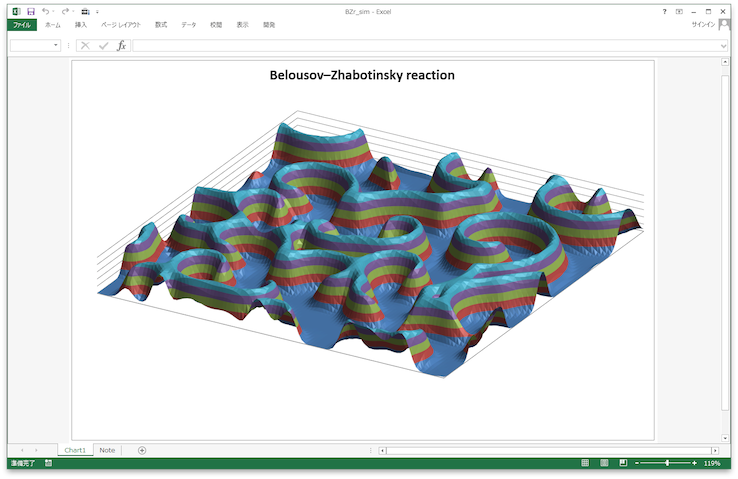
(設定画面と計算された濃度の空間分布。ランダムな初期状態から十分な時間が経過した後の濃度分布の状態。濃度を高さで表現して立体的に図示している。)
B-Z反応シミュレーション用エクセルファイル BZr_sim.xlsm
このエクセルファイルでは平面上の厚さのうすい条件でのB-Z反応を再現しているので、実際の計算も水平2次元で行われています。平面を100 x 100 = 10000個のメッシュに分割して、拡散と反応を計算しているので、単純化しているとはいえ、計算には時間がかかります。本来、100 x 100程度のサイズでは空間分解能としては不十分ですが、エクセルVBAの計算速度やグラフの処理能力の関係であまり大きくはできません。これ以上の計算は、エクセルには荷が重すぎます。もっと分解能を高くするにはどうすれば良いでしょうか?さらに、理論計算上はこれを3次元空間に拡張することもできます。3次元空間でB-Z反応が起こる場合には、平面の場合に現れるターゲット・パターンやスパイラル・パターンはどうなってしまうのでしょうか?より大きなサイズの平面や、3次元空間でのB-Z反応を再現しようすると、計算はケタ違いに膨大なものになり、もはやエクセルVBAでは対応できなくなります。そのような目的のためには、例えばFORTRANやCのような、より高速で数値計算に適した言語で計算プログラムを作る必要があります。以下に、C++を用いて計算したB-Z反応シミュレーションの結果をいくつか示しました。今のパソコンでも当たり前になったマルチコアプロセッサと、並列計算の技術を使うと、3次元空間における100 x 100 x 100 = 100万個のグリッド上での拡散・反応の計算を100回繰り返すのに、わずか数秒しかかかりません。
(3次元B-Z反応シミュレーションの結果。立方体を100 x 100 x 100のグリッドに分割。図は10000回の計算ステップ後の濃度分布をグレースケールで表しています。)
3次元B-Z反応時間発展を動画にして、一例としてこちらに紹介しています(GIFアニメ11.7MB、300ステップまで)。
(2次元B-Z反応のシミュレーションの結果。平面を3000 x 3000 = 9百万のメッシュに分割。図は10000回の計算ステップ後の濃度分布をグレースケールで表しています。)
(上の図の一部分を拡大した様子。規則的なスパイラル・パターンが見られます。唐草模様にそっくりです。)
いずれも計算条件は以下の通り。
Intel Xeon(R) E3-1240 v3 4コア8スレッド
g++ 4.8.2 / OpenMP (8スレッド)/ コンパイルオプション -fopenmp -O3
計算時間は、3D(100 x 100 x 100) 、1万ステップが380秒、2D(3000 x 3000)、1万ステップが3770秒。
デイジーワールド
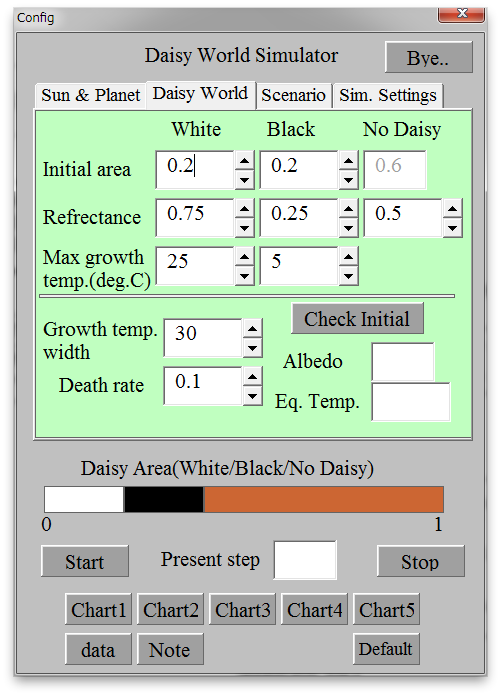
デイジーワールド、つまりヒナギクの世界、とは仮想的で単純な惑星表層環境の数理モデルです。惑星表面に白色と黒色の2種類のヒナギクが存在し、それぞれの生存圏の面積は惑星の温度に応じて変化する増殖率、それぞれの占有面積、自然死の割合によって支配されます。ロトカ・ヴォルテラ方程式でも同じですが、自己の存在量に比例して増殖する自己増殖モデルは、いわゆるネズミ算式と同じです。さらに、有限な惑星表面を占有する競合過程と、増殖率が一定温度範囲のみで値をもち、かつ、最適温度が存在する、というあたりが生命活動を最もシンプルにモデル化しているところです。白いヒナギクは太陽放射に対する反射能が高いので、太陽放射が強いときに白いヒナギクの面積が拡大すれば、より太陽放射を反射することで惑星の温度上昇を抑制することができます。黒いヒナギクでは逆もまたしかりです。ある瞬間のヒナギクの占有面積が決まると、それぞれの反射能に面積比を乗ずることで、惑星のアルベドが決まります。惑星アルベドが決まれば、惑星が受ける太陽放射エネルギーと失う赤外放射エネルギーのバランスの変化によって、惑星の温度は新たな放射平衡温度に向かって変化します。これと似たようなフィードバックは雪氷圏にもあり、気候学ではそれを「アイス-アルベド・フィードバック」と呼んでいます。ただし、その場合には、低温でアルベドが高くなり、高温でアルベドは低くなる、というやや単純な関係が想像できます。生命モデルの場合には、上記のようにさらに複雑なフィードバックになりますので、いわば「バイオ-アルベド・フィードバック」ということができるかもしれません。このようなシステムにおいて、外的強制として太陽定数を変化させたとき、惑星の温度はどうなるか、というのが問題です。このデイジーワールドは、ガイア仮説を提唱したラブロックが、その仮説の妥当性を示すために作ったものです。その結果は、生命のない惑星では太陽定数の変化に追随して単調に温度が変化するのに対して、ヒナギクの世界では一定の範囲で太陽定数が変化している間は2つのヒナギクの占有面積が変化してアルベドを変えることによって惑星の温度を安定化させる、というものです。その温度の安定化はヒナギク自身の増殖可能な温度範囲内で行われるため、生物のもつ重要な働きになぞらえて、システムがホメオスタシス(恒常性)を持つものと説明されています。したがって、例えばヒナギクの種類を増やすというようにフィードバックをさらに複雑にしてゆくと、システムのホメオスタシスがさらに強化されることも理解できます。さらに拡張を加えて、例えば大気成分を変化させて温室効果を考慮したり、前述の雪氷圏を組み込んだり、ロトカ・ヴォルテラ方程式のように生物同士のフィードバックを入れたりすることもできます。
かれこれ30年くらい前、当時使っていたモノクロ画面の四角い筐体のMacに、なぜかDaisy Worldのソフト?が入っていました。地球環境を題材にした数理モデルに私が接したのはこれが最初だったように思います。このころ、ラブロックのガイア仮説は地球科学の範疇を超えた世界で語られることが多く、少し拡大解釈を伴って世間に広く流布されていたように思います。私は非線型システムとしてのDaisy Worldに興味を持ち、地球表層のような複雑な要素間でフィードバックをもつシステムにサイバネティクスやホメオスタシスという概念を導入した点に感動していました。その後、時が過ぎ、職を得て以降、学生教育を目的として、あまり出来映えは良くないのですが、Daisy Worldのプログラムを何度か自分で作成しました。そしてまた、性懲りもなくエクセルVBAで作ってしまいました。
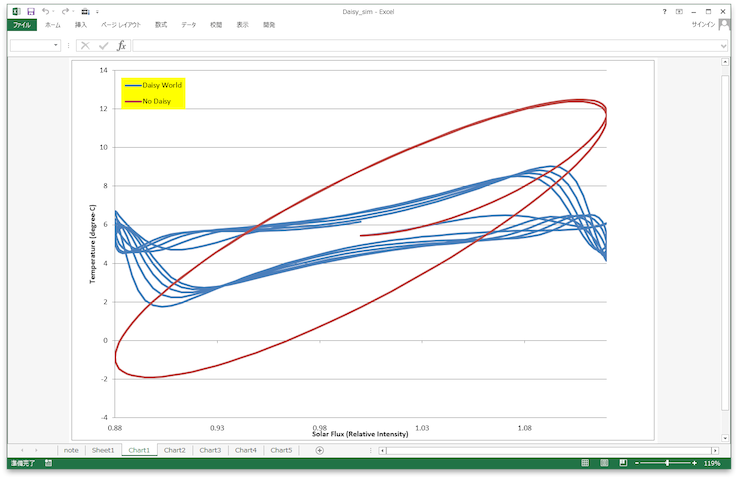
(設定画面と計算結果。太陽定数の周期的な変化に対する温度の応答の例。熱容量を仮定して温度の時間積分を行っているため、生命がない場合(赤色)でもヒステリシスがあるが、デイジーワールド(青色)ではより複雑なヒステリシスが見られ、同時に、温度の変化の幅が小さくなっていることがわかる。)
デイジーワールド シミュレーション用エクセルファイル Daisy_sim.xlsm
追記(2021/9/9)
R+Shinyを使って、デイジーワールドシミュレータを、shinyapps.ioにデプロイしたウェブアプリとして作成しました。私にとっては5つ目の言語で作成したデイジーワールドになります。
エクセルファイルについて
ここで公開しているMS Excelのファイルは、拡張子がxlsmの「マクロ有効ブック」の形式になっています。ダウンロードして始めて使用する際には、マクロが含まれていることの警告が表示されたり、初期はマクロが無効になっているはずです。シミュレーションを実行するためには、マクロを有効化してお使いください。動作確認はExcel 2013、Excel for Mac 2011で行っています。古いバージョンのExcel 2003でも一部を除いて動作するようです。マクロの実行速度はマシンに依存します。また、一般にExcel for Macではマクロの実行速度が遅くなるようです。VBAプロジェクトはプロテクトをかけていますので、コードの編集はできません。コードの開示は個別のご相談に対応します。
(免責事項)ここに公開しているマクロ付きのエクセルファイルをダウンロードしてご使用することによって生じる如何なる損害についても当方は責任を負いかねます。